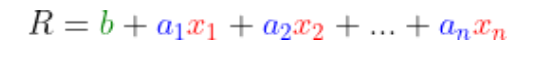L’expérience montre que cela n’est pas suffisant. D’ailleurs, les régulateurs des établissements financiers ne se contentent pas de savoir qu’un modèle peut permettre de réduire le taux de défaut sur des prêts. Ce qu’ils veulent savoir, c’est pourquoi une décision spécifique a été prise.
Alors, comment obtenir des informations de la part d’un modèle pour qu’un utilisateur non technique puisse évaluer la pertinence du modèle ?
Un modèle simpl(ist)e
La régression logistique
La plus simple des solutions pour fournir une explication simple à un tiers est d’utiliser un modèle dont la structure est elle-même facile à expliquer. La régression logistique est un des premiers modèles statistiques utilisé. Elle est simple à concevoir, est facile à optimiser et ne nécessite pas de grosses ressources informatiques.
Une rapide recherche web sur la régression logistique peut entraîner les plus allergiques aux mathématiques à penser que la simplicité annoncée de la régression logistique n’est qu’un leurre.
En fait, derrière cette expression mathématique alambiquée se cache des concepts extrêmement accessibles. Le cœur de la régression logistique est une somme pondérée telle que la formule ci-dessous. Les variables x sont les variables descriptives utilisées dans le modèle.
Par exemple, il peut s’agir des caractéristiques d’une maison dans un modèle de prédiction de prix immobilier. Les variables a et b sont les coefficients du modèles. C’est la valeur de ces variables que l’on va chercher à optimiser pour que R soit le plus proche possible du prix réel de la maison, pour toutes les maisons que l’on a dans notre base de données.
Dans cette formule, R peut prendre n’importe quelle valeur. Dans une régression logistique, on fait passer R dans une autre formule mathématique, la fonction logistique, pour s’assurer que R soit entre 0 et 1. Pour résumer, la régression logistique est une somme pondérée des variables descriptives, ramenée à des valeurs entre 0 et 1.
Titanic : un modèle d’application
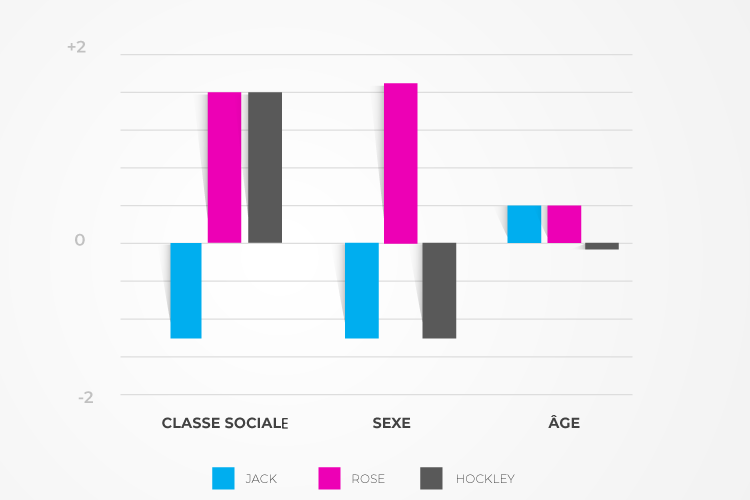
Prenons comme exemple le dataset de prédilection des apprentis data scientist : les données sur les passagers du Titanic. Dans ce célèbre tutoriel, on essaie d’identifier les rescapés de ce terrible naufrage. On va considérer ici un cas simple utilisant simplement la classe social, le sexe et l’âge du passager. Comparons les prédictions de notre petit modèle pour les trois protagonistes du célèbre film de 1999.
Le héros du film, Jack, est un homme de troisième classe. Le modèle attribue une contribution négative à ces caractéristiques pour les chances de survie de Jack. En revanche, Rose est une femme de première classe et bénéficie donc du célèbre adage « Les femmes et les enfants d’abord » (le modèle n’est pas entraîné pour savoir qu’elle sautera de la barque à la dernière seconde).
Hockley, le fiancé de Rose, ne bénéficie pas de la priorité pour monter à bord des barques de sauvetage en tant qu’homme. Par contre, son statut de passager de première classe semble améliorer ses chances. Plusieurs scènes montrent en effet des hommes de première classe dans les barques, pas seulement notre antagoniste.
Le modèle montre ainsi une cohérence avec nos attentes : les femmes et les enfants d’abord, les privilèges de la première classe, etc. Ainsi, bien que les paramètres du modèle aient été optimisés en dehors de toute « expertise » externe, nous pouvons vérifier que son comportement est cohérent avec les attentes des « experts ». À travers ce travail d’étude de l’explicabilité, nous gagnons en confiance vis-à-vis du modèle.
Une technique pour les expliquer tous
Lorsque l’on souhaite utiliser des modèles plus complexes, l’explicitation directe du modèle telle que nous venons de la faire n’est alors plus possible. De nombreuses méthodes ont alors été développées pour tenter d’identifier les éléments dominants du résultat. La méthode la plus populaire aujourd’hui repose sur la valeur de Shapley.
La valeur de Shapley
En théorie des jeux, la valeur de Shapley permet de déterminer la manière de répartir de manière « juste » parmi les participants les gains d’une activité collective.
L’exemple proposé dans cette vidéo explicative repose sur un voyage en taxi commun. Trois personnes partagent un taxi. Le trajet coûte moins cher que la somme de trois voyages individuels. Comment peut-on alors répartir équitablement le “gain” lié au partage du taxi ? En attribuant à chaque personne la fraction du gain correspondant à sa valeur de Shapley. Cette vidéo (cette fois en Français) propose une autre étude de cas.
Dès qu’un modèle devient un peu complexe, les variables peuvent avoir des effets combinés. Dans le modèle précédent, l’impact de la classe était identique, quel que soit le sexe de la personne. Cependant, on peut facilement imaginer que la différence homme/femme dans les chances de survie soit beaucoup plus marquée en troisième classe plutôt qu’en première. Il devient alors difficile d’estimer la contribution de chaque variable indépendamment.
La valeur de Shapley permet de répondre à cette problématique. Pour une personne donnée, on peut calculer les chances de survie si on ne considérait qu’un sous ensemble des caractéristiques disponibles.
Par exemple on peut calculer ses chances sans considérer le sexe ni la classe de la personne. On répète ensuite l’opération pour tous les sous-ensembles possibles.
En faisant des moyennes pondérées des chances de survie (méthode de Shapley) pour chaque sous ensemble, on est capable d’obtenir l’importance de chacune des variables pour cette personne spécifique.
La compréhension des techniques de data science par les métiers comme clé de la confiance
Une méthode (plutôt populaire) a été détaillée ici. Il en existe beaucoup d’autres, quelques fois spécifiques à un domaine (analyse d’image …). Ici, les détails d’une technique sont moins importants que le pourquoi des détails.
Il a été déjà mentionné que la confiance des experts métier dans les systèmes d’IA passe en partie par l’explicabilité. Le métier pourrait tout à fait se contenter des explications brutes fournies par une méthode donnée.
Cependant, les modèles d’explication ne donnent qu’une image biaisée de la réalité du modèle. Pour Shapley par exemple, la contribution de chaque variable dépend des caractéristiques de notre passager anonyme.
Il est alors important que les experts métiers aient des notions sur les modèles employés ainsi que sur leurs techniques de visualisation pour pouvoir collaborer toujours plus efficacement à la création de modèles utiles.